Amostragem e Tamanho de Pixel - Parsec
Parsec.net
Amostragem e Tamanho de Pixel
Astrofotografia > CCD's e etc
Tamanho do Pixel do Sensor
Todo sistema de imageamento astronômico (Image Astronomical System - IAS) tem por finalidade primária a coleta de fótons (luz) com objetivo de reproduzir a imagem do objeto no plano focal. Considerando uma fonte puntual, por exemplo uma estrela, a imagem formada no plano focal consiste de uma região central brilhante circundada por anéis escuros e anéis com brilho variável, estes últimos diminuindo de intensidade a medida que nos afastamos da região central. Este padrão é o que denominamos de PSF (Point Spread Function) ou Função de Espalhamento Puntual. O disco central é conhecido como disco de Airy (Figura 1).

Figura 1 - Disco de Airy Central e padrão PSF.
Em um telescópio opticamente "perfeito" e não obstruído, em condições ideais de observação, o disco de Airy contém 84 % da energia radiante do objeto com os outros 16 % restante distribuídos pelos anéis brilhantes (veja PSF e Seeing). Como a maior quantidade de energia esta concentrada no disco de Airy, este é a imagem da fonte puntual que desejamos registrar em nosso sensor.
No disco de Airy, metade da energia luminosa esta concentrada em um núcleo central no interior de uma região denominada de FWHM (Full Width Half Maximum) ou Máximo da Metade da Largura Total (veja PSF e Seeing). A imagem puntual de uma estrela representa a menor unidade significante que podemos registrar. Assim:
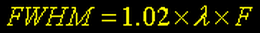
Equação 1
Da equação acima, podese observar que p FWHM depende do comprimento de onda (l) da luz incidente e da razão focal (F) do IAS. Consideremos o seguinte exemplo: um telescópio newtoniano com abertura de 200 mm e razão focal F/6 é utilizado para fotografar a nebulosa de Órion (M42) no comprimento de onda do oxigênio duplamente ionizado (OIII). Pergunta-se: qual seria o tamanho de pixel mais adequado?
Considerando que as linhas espectrais do oxigênio duplamente ionizado possuem seu máximo de emissão em 496 e 501 nm, podemos pegar qualquer um desses valores, já que a variação será desprezível. Colocando os valores na equação 1, teremos:"
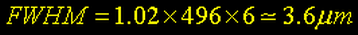
Assim, o tamanho de pixel ideal para registrar as emissões na linha do oxigênio duplamente ionizado é de aproximadamente 3.6 micra. Naturalmente, isto é computado para condições ideais.

Figura 2 - Nebulosa de Órion (M42), fotografada através de um telescópio William Optics ZS 66, F/5.9. Exposições: 7 x 300 seg (H-alpha), 10 x 200 seg (SII, bin 2x2) e 13 x 200 seg (OIII, bin 2x2). Exposição total de 1h 50 m. Crédito: João Vieira, Torres Nova, Portugal, 2007.
Teorema de Nyquist
De acordo com o Teorema de Nyquist, a quantidade de amostras por unidade de tempo de um sinal, chamada taxa ou freqüência de amostragem, deve ser maior que o dobro da maior freqüência contida no sinal a ser amostrado, para que possa ser reproduzido integralmente sem erro de aliasing.

Figura 3. Harry Nyquist, 07/02/1889 - 04/04/1976. Crédito Imagem: Wikipedia.
 ?????!!!!!!
?????!!!!!!Todos os sensores digitais são organizados na forma de matrizes de pontos foto-sensíveis e as imagens projetadas por uma objetiva sobre estes sensores são contínuas. Isto por si só constitui um problema. Precisamos representar uma informação contínua (a imagem do objeto) em um meio descontínuo de maneira que esta informação permaneça reconhecível. A informação contínua deve então passar por uma amostragem (sampling), que de uma maneira bastante simples é equivalente a “fatiar” a informação contínua em amostras “discretas”, que tem um determinado “valor” numérico.
Imagine um sensor monocromático, composto por uma matriz de pontos, e que registre apenas se o pixel foi iluminado ou não, independentemente de sua cor. Imagine agora uma imagem sendo projetada, perfeitamente em foco sobre este sensor. Suponha que a imagem projetada seja Saturno, observado através do telescópio. O resultado é que esta imagem não pode ser representada perfeitamente pela matriz e se você prestar atenção, vai observar que a imagem resultante é formada por quadrados apresentando-se “serrilhada” (Figura 4). Este fenômeno chama-se “aliasing” que provém da perda e distorção da informação contínua original, quando representada em uma forma discreta.

Figura 4. Ampliação de uma imagem de Saturno mostrando o efeito de aliasing. Crédito da Imagem: Conrado Seródio.
O termo correto em português para aliasing é freqüências réplicas, mas como é pouco difundido, utiliza-se o termo inglês aliasing.
O “aliasing” é causado pela insuficiência de resolução (número de amostras ou samples) capaz de representar de maneira satisfatória uma imagem.
Note que qualquer processo de conversão de uma informação contínua (analógica) em uma informação discreta (digital) acarreta em perdas, e esta perda pode ser reduzida com o aumento de amostras. No caso de imagens, estamos falando de píxeis e a resolução de uma imagem é espacial.
O interessante é que, no caso dos filmes fotográficos (sim, os filmes de celulóide), o aliasing é extremamente diminuto ou mesmo inexistente. Isso ocorre porque a resolução espacial do filme fotográfico é enorme, e também porque a disposição dos grãos é aleatória.
O problema, então, é determinar quantos píxeis são necessários para representar a imagem original?
Para uma função gaussiana PSF bidimensional, como o caso da imagem estelar, o teorema de Nyquist é FWHM = 3.3 píxeis.
Amostragem Otimizada
Quando falamos de amostragem otimizada é necessário nos perguntarmos o que esta sendo otimizado? Há pelos menos quatro pontos que podemos otimizar:
- Resolução
- Campo de visão
- Relação Sinal/Ruído para Objetos Difusos
- Relação Sinal/Ruído para Objetos Brilhantes
Naturalmente, seria desejável otimizar todos ou quase todos parâmetros. Infelizmente cada parâmetro acima possui um critério de amostragem ótimo diferente, de modo que, é importante avaliar cada abordagem de acordo com a importância que terá na escolha do tamanho de pixel adequado para um determinado fim.
A amostragem otimizada para o campo de visão é bastante simples. Basta considerar o tamanho do pixel e a distância focal para se obter o campo de visão desejado. Você pode utilizar a calculadora disponível em The New CCD Astronomy ou, se preferir, usar uma on-line.
As abordagens referentes a otimização da relação Sinal/Ruído é bastante complexa e demanda um tratamento mais profundo. No entanto, duas observações podem ser destacadas:
- Otimização Sinal/Ruído para objetos difusos beneficia-se de um quantidade de píxeis por objeto geralmente abaixo do número mínimo de píxeis necessários para reter a resolução intrínseca do objeto, tirando proveito do "under-sampling" (sub-amostragem).
- Otimização Sinal/Ruído para objetos brilhantes beneficia-se de um quantidade de píxeis por objeto geralmente acima do número mínimo de píxeis necessários para reter a resolução intrínseca do objeto; tirando proveito do "over-sampling" (sobre-amostragem) e melhorando a precisão fotométrica de objetos brilhantes.
Otimizando Amostragem para Resolução
Há muita controvérsia nos círculos de astrofotógrafos no que diz respeito ao mínimo de amostragem necessária de modo a preservar a resolução. O critério de Nyquist do dobro da amostragem do sinal analógico é frequentemente evocado e aplicado como exemplo crítico, isto é, a Amostra = 2 x FWHM.
Entretanto, o critério de Nyquist é específico para se obter o mínimo de amostragem do sinal necessário para capturar e reconstruir uma onda senoidal de audio. A solução mais comum do critério de Nyquist é a largura (desvio padrão) da função, que para uma gaussiana é FWHM = 2.355 pixels. Mas este valor é tomado de um único eixo e para medir a resolução através da diagonal de um pixel quadrado, é necessário multiplicar este valor pela raiz quadrade de dois, o que resulta em FWHM = 3.33 pixels
Este valor é mais realista, uma vez que a maioria dos telescópios não produzem uma gaussiana PSF pura e assim pode-se ter uma certa margem de manobra. Outro problema é que se realiza diversas reamostragens de modo a se ter diversas imagens que serão combinadas. Esse processo pode gerar turvação da imagem e perda de informação, principalmente se tivermos amostrando no limite mínimo.
A teoria prediz e, realmente ocorre, uma leve degradação da imagem quando FWHM = 3.0 pixels e uma degradação significante quando FWHM = 1.5 pixels. Um equipamento amador típico pode produzir imagens com FWHM entre 2.0 e 3.5 arcsec; assim, um tamanho de pixel de 0.5 a 1.5 arcsec pode ser considerado ideal para otimização da resolução.
CCD's - ALGUNS DETALHES
Alguns detalhes sobre CCD's antes de prosseguirmos.
Fótons - CCD's são semicondutores de silício que apresentam uma estrutura tal que formam corredores elétricos localizados de modo que um fóton - um pacote de energia - ao ser absorvido pelo substrato de silício é conduzido como um elétron por estes corredores para um ponto espacialmente localizado denominado "píxel". Quando o dispositivo é lido, a linha superior é serializada através de um pré-amplificador, amplificador e u8m conversor analógico/digital. A seguir todas as linhas são deslocadas para cima e lidas sequencialmente. Mantendo-se o controle de leitura bidimensional, a matriz bidimensional pode ser reconstruída totalmente após a serialização (Figura 5).
Elétrons - Os elétrons acumulados em cada pixel são representados por um número em unidades de DN (Data Number) pu ADU (Analogue to Digital Unit - A/D). Em geral são utilizados 16 bits para representar esse número (DN), mas isso pode variar de acordo com o CCD.

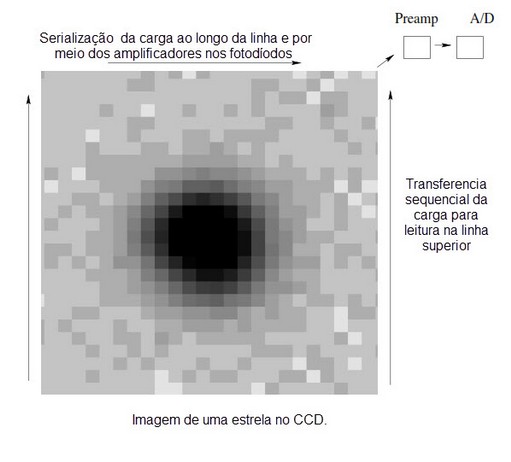
Figura 5. - Processo de leitura de um CCD.
Assim, a faixa dinâmica que uma câmera CCD utilizando um conversor A/D com 16 bits poderá alcançar é de:
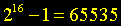
Quanto maior a faixa dinâmica, mais informação pode ser registrada. Uma webcam possui um conversor A/D com 8 bits; já uma câmera dedicada para astrofotografia pode conter um conversor A/D de 8 bits, 12 bits, 14 bits, 16 bits ou 24 bits. Naturalmente, quanto mais bits forem utilizados pelo conversor A/D para representar de forma discreta a informação analógica maior será a sua precisão e também o custo final da câmera.
Ganho-Inverso - quase sempre referido apenas como Ganho - G - é um fator de conversão estranho mas em unidades adimensional de:
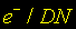
O Ganho é um fator que frequentemente pode ser alterado. Entretanto, como saber qual fator de Ganho a ser utilizado? Isso depende do tipo de dado que você pretende registrar. A escolha recai sobre a faixa dinâmica e a leitura de ruído efetiva, embora exista problemas sutis com alguns tipos de chips.
Resumindo:

- Usualmente estaremos trabalhando em distâncias focais acima de 2000 mm. No caso de astrofotografia planetária, razões focais de 6000 mm ou maiores é bastante comum.
- Selecione a amostragem que melhor se adapte a sua melhor condição de seeing no seu local de observação.
- Multiplique por 3 para ser mais realista com a sua melhor condição de seeing.
Exemplo: as melhores condições de seeing nos últimos 4 anos em determinado sítio observacional foi em média 1,6" FWHM com um telescópio newtoniano de 381 mm de abertura, utilizando uma lente barlow e resultando em 3000 mm de distância focal com câmera CCD SBIG, modelo ST10XME, tamanho de pixel de 6.8 micra, resultando em uma amostragem de 1.6/3 = 0.53".
Como pode ser observado, é importantíssimo que você possua um "logbook" de suas observações; isto é, você precisa ter um planejamento detalhado e registro das condições observacionais do seu sítio de observação. Em ciência trabalhamos em cima de dados. Sem isso, não há como controlar seus experimentos. Se você não sabe o que é seeing, veja Seeing Astronômico.
Se você não possui um logbook, providencie um ou adquira um na internet. Existe programas como Sky Tools, Deep Sky Planner, DeepSky, e outros comerciais que permitem o planejamento de sessões observacionais e registro de seus resultados de observação. Também existem logbooks gratuitos, tanto para sistemas Windows como para Linux. Procure pelo Google com o termo "astronomy logbooks" ou algo parecido e muitos serão listados. Escolha o que melhor você se adapta. E por último, por que não criar seu próprio logbook.
Para calcular a amostragem, considerando o tamanho de píxel do CCD da câmera e o IAS, podemos usar a seguinte equação:

No exemplo acima, teríamos:
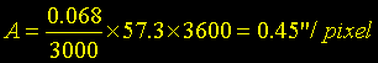
Para adequarmos as condições de seeing, multiplicamos esse valor por 3 (0.45" x 3 = 1.35"). Mesmo com esse resultado, é pouco provavel que consigamos atingir tal valor na maioria das noites de observação devido a diversos fatores como, turbulência da atmosfera, óptica deficiente, e outros.
Em sítios observacionais urbanos, o valor do seeing em sua melhor condição, dificilmente será superior a 2" de arco. Sítios em áreas mais remotas podem atingir 1" de arco. Assim, pode-se observar o seguinte quadro:

Resolução Máxima do Telescópio
Pelo critério de Rayleigh, e isto é vital para astofotografia planetária, a máxima resolução do telescópio pode ser calculado com a seguinte equação:
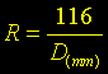
Onde D é a abertura do telescópio em milimetros, obtendo-se R em segundos de arco. Assim:

Pelo critério de Sparrow, não muito realista para objetos de céu profundo (DSO), mas aplicável ao imageamento planetário com óptica perfeita; podemos calcular a resolução por meio da equação:
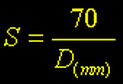
Assim:

Deste modo, procure utilizar video-câmeras com o menor ruído que você possa obter. Este é o melhor meio de se obter a exposição da sorte (lucky frame); isto é, a exposição naquele momento ideal de melhor seeing.
A distância focal do telescópio deve ser aquela em que você obtenha o máximo da resolução (veja o critério de Sparrow e as equações acima).
O critério de Sparrow de resoluções extremas parece ser realista em astrofotografia planetária. Naturalmente, um seeing deficiente sempre irá limitar severamente este critério. Por outro lado, mesmo com o melhor seeing, o critério de Sparrow não se aplica a objetos de fundo de céu (DSO).
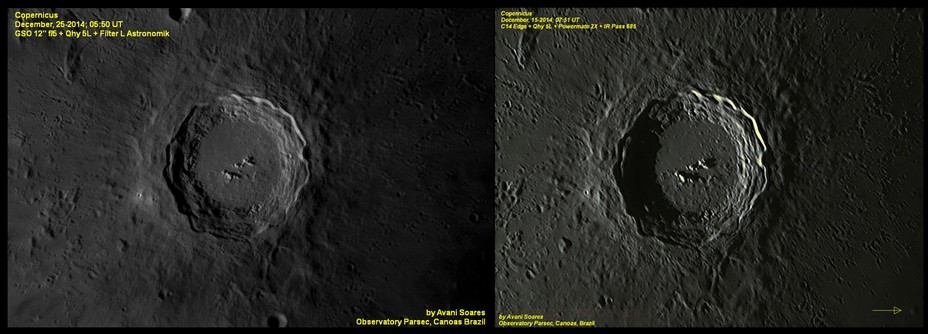
Figura 6. Cratera Copernicus. Imagem a esquerda realizada com um telescópio GSO, newtoniano de 305 mm, F/5, utilizando uma Powermate 2X. Imagem a direita realizada através de um Celestron C14, 355 mm de abertura, F/11, utilizando uma Powermate 4X. Crédito: Avani Soares.
