PSF e o Seeing - Parsec
Parsec.net
PSF e o Seeing
Astrofotografia > CCD's e etc

Função de espalhamento pontual (Point Spread Function - PSF) descreve a distribuição bidimensional da luz de objetos astronômicos pontuais no plano focal do telescópio. Os desenhistas ópticos fazem um grande esforço em reduzir o tamanho da PSF para os grandes telescópios, uma vez que a PSF é um ponto crítico para os instrumentos projetados de modo que seu desempenho seja muito próximo ao limite de difração.
Naturalmente, esse esforço esta presente na fabricação de telescópios que são destinados à operarem no espaço; mas também aparece nos modelos de telescópios mais sofisticados, utilizados pela comunidade de astronômos amadores ao redor do mundo.
A PSF é grandemente afetada pelos efeitos do "seeing" e também do foco do telescópio. A tecnologia permite obter um foco com maior precisão, utilizando-se de focalizadores automáticos e complexos e de sistemas de óptica adaptativa ou ativa, para reduzir os efeitos do seeing sobre a PSF.
A PSF para um sistema óptico perfeito, baseado em elementos circulares, seria um "padrão de Airy" ou "disco de Airy", derivado da teoria de difração de Fraunhofer (uma aproximação escalar aplicada ao plano de ondas).
O Padrão de Airy é dado pela equação:
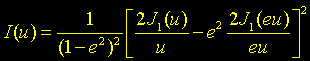
Onde, I(u) é o brilho de superfície no plano focal, normalizado para seu máximo em u = 0; u é a distância adimensional do eixo óptico no plano focal correlacionado ao raio angular theta (ϴ) (medida da abertura primária) e o diâmetro D da abertura primária, obtido da equação:
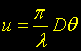
A variável "e" é a obstrução da apertura primária (assumindo ser circular) e pode ter valor zero. J1 é uma função besseliana de primeira ordem.
Assim, toda imagem de uma fonte puntual, por exemplo, uma estrela, produz uma imagem que é de fato um artefato de difração. Este artefato é devido a natureza ondulátoria da luz e o fato de que a sobreposição das ondas pode levar a uma maior amplitude, por exemplo, quando dois picos se sobrepõem; ou a uma amplitude zero, por exemplo, no evento de sobreposição de um pico com um vale. Estes eventos são responsáveis pelo padrão de luz e ausência de luz (escuridão) no artefato de difração, como na imagem abaixo (newtoniano 200 mm, F/6, não obstruido, 550 nm):

O tabela abaixo mostra os maiores dados característicos de um padrão dse Fraunhofer não obstruído para aberturas circulares. Estão tabelados a posição, intensidade relativa e a percentagem de energia total correspondente a cada anel ou banda:
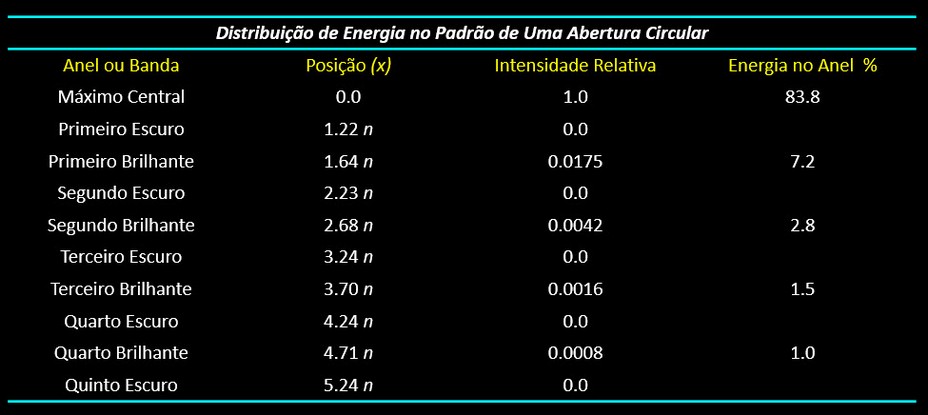
Como pode-se observar na tabela acima, o máximo central e o primeiro anel brilhante da figura de difração, contém praticamente toda energia luminosa que foi focalizada no sistema de imageamento, considerando este como circular e sem nenhuma obstrução, por exemplo, a objetiva acromática de um telescópio refrator. A presença de uma obstrução central, como ocorre em telescópios newtonianos e catadióptricos, altera a figura de difração e, consequentemente, a distribuição de energia pelos anéis do artegato de difração.
O tamanho relativo deste artefato é determinado pela abertura da objetiva do telescópio (objetiva acromática ou espelho primário), sua qualidade óptica e o comprimento de onda da luz. Telescópios com melhor qualidade óptica e maiores aberturas produzem um artefato de difração menor e mais concentrado. Mas independentemente do seu diâmetro angular, o artefato tem uma forma invariável em seção transversal, que pode ser caracterizada por uma curva gaussiana ou normal, com um pico central, forte inclinação lateral, e uma série de platôs menores resultante dos anéis concêntricoss (figura abaixo). (Observe que a escala horizontal é padronizada sobre o diâmetro de abertura D e o comprimento de onda da luz.)
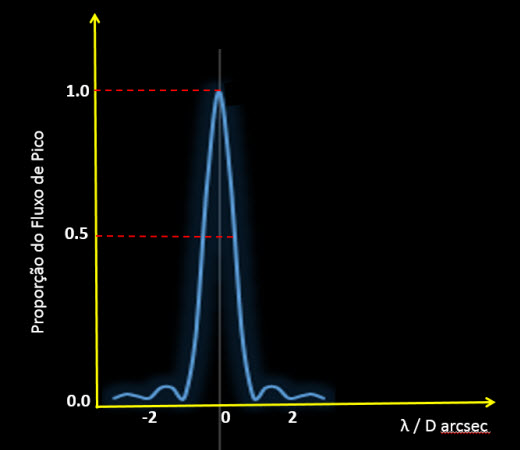
A curva no gráfico anterior não representa uma curva da distribuição da luz, mas uma distribuição de probabilidades de que um único fóton atingirá um receptor em um local específico. Como o número total de fótons captados pelo receptor aumenta, por exemplo, por aumentar o tempo de exposição ou por imagear um objeto brilhante, a distribuição torna-se mais representativa. No entanto, não se torna mais amplo a medida que a luz acumula, apenas torna-se mais alto. Como resultado — em condições ideais, as proporções relativas horizontais da distribuição permanecem constantes. Isso é ilustrado no gráfico abaixo, que mostra que há uma relação constante entre o raio medido do artefato e a proporção de energia luminosa que contém o raio.
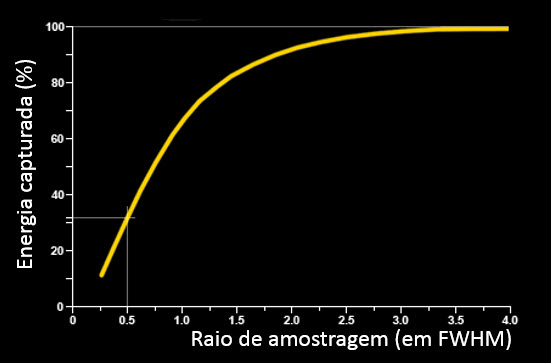
Um método simples para fazer medidas equivalentes das distribuições Gaussianas, independentemente da quantidade de energia luminosa que eles contêm, é o método do máximo da metade da largura total - FWHM - Full Width Half Maximum. O pico ou o valor máximo da distribuição (em lúmens, ADUs ou qualquer outra medida de energia luminosa) é dividido ao meio, e a largura da distribuição é medida. O resultado pode ser visualizado na figura abaixo:
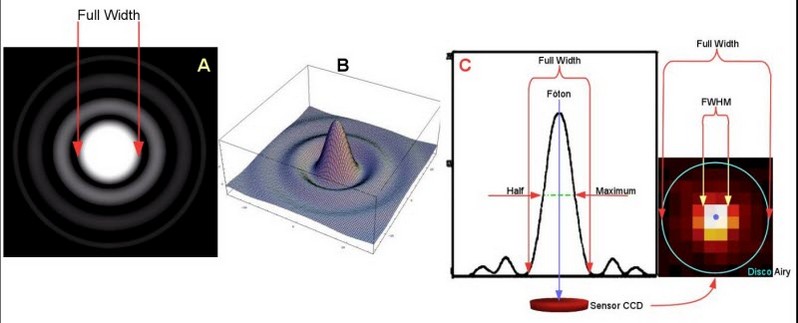
Em A, temos a figura de difração ou disco de Airy, onde o círculo central brilhante é a largura total (Full Width). B é uma representação tridimensional da figura de difração, enquanto que em C, temos a sua representação gráfica bidimensional posicionando os componentes em relação a figura de difração e suas partes incidentes sobre um sensor CCD. Pode-se observar que a área de captura da FWHM é bem mais concentrada que a área da FW que se espalha por mais pixels resultando em uma figura difusa e de baixa resolução.
O seeing tem grande importância na astrofotografia pois afeta diretamente a figura de resolução acima mostrada. Devido a turbulência atmosférica e as diferentes temperaturas nas camadas de ar que resultam em diferentes densidades e, consequentemente, em índices de refração diferentes; temos que a figura de difração é na realidade composta por um aglomerado de figuras de difração refratadas. Como resultado, a fonte de luz puntual não apresenta uma única distribuição em um local fixo, mas se espalha em torno do ponto principal. O resultado é uma imagem difusa que possui um diâmetro muitas vezes maior do que a distribuição Gausiana. A figura abaixo ilustra esse efeito:
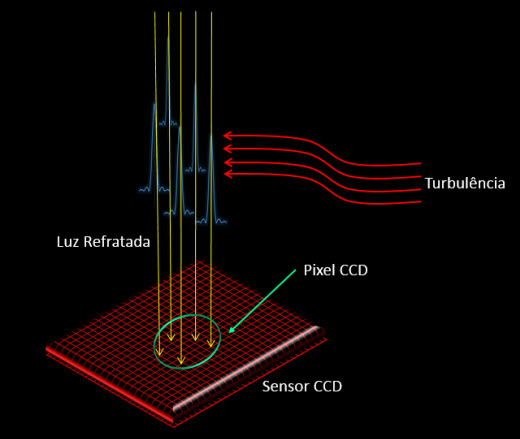
Assim, uma boa estabilidade atmosférica, isto é, um bom seeing vai apresentar um FWHM concentrado e de melhor resolução.


