Tempo Máximo de Imageamento - Parsec
Parsec.net
Tempo Máximo de Imageamento
Astrofotografia > CCD's e etc
Tempo Máximo Teórico de Imageamento
As imagens planetárias de alta resolução realizadas por diversos amadores espalhados ao redor do globo seguem uma mesma técnica de obtenção: o alinhamento, por meio de um programa de computador, dos diversos fotogramas componentes de um único filme. Este filme, geralmente no formato AVI (Audio Video Interleave), em uma tradução livre, algo como “mistura de vídeo e áudio”, é composto por diversos fotogramas (quadros) adquiridos geralmente em 5 a 15 FPS (Frames per Second – Quadros por Segundo) com duração de alguns segundos a poucos minutos, através de uma câmera. Assim, podemos ter de centenas a milhares de fotogramas em um filme, dependendo do tempo de filmagem.
O problema é que, todos os planetas realizam o movimento de rotação em torno do seu eixo, em maior ou menor velocidade dependendo do planeta. Assim, o tempo de filmagem deve ser tal que a rotação do planeta não seja detectada causando deterioração da imagem. Como determinar esse tempo é o cerne da questão.
Fatores Limitantes
A duração máxima da filmagem em alta resolução de um planeta é afetada por diversos fatores, dentre estes:
- O planeta alvo da filmagem à Júpiter, por exemplo, possui uma rotação muito rápida. Como o planeta apresenta velocidades de rotação diferentes nas regiões mais próximas ao equador ou ao pólo, utilizam-se dois sistemas principais. O Sistema I é utilizado para as regiões localizadas dez graus ao norte ou ao sul do equador do planeta e possui uma rotação de 09 horas e 50 minutos.
- O Sistema II é para latitudes norte e sul desta região e a rotação é de 09 horas e 55 minutos. O Sistema III, mede a velocidade de rotação da magnetosfera de Júpiter e é considerada a velocidade de rotação oficial do planeta.
- O tamanho angular aparente do planeta.
- A distância focal efetiva do sistema de astrofotografia.
- As especificações do sensor da câmera (tamanho e número de pixels).
O resultado final ainda depende das condições do sítio de observação e, logicamente, da qualidade óptica do equipamento utilizado.
Cálculo
Na figura 1, representando um planeta visualizado de acima do seu pólo e de frente de modo que seu movimento de rotação seja contra os ponteiro do relógio em torno do seu eixo o qual se localiza no centro do círculo.
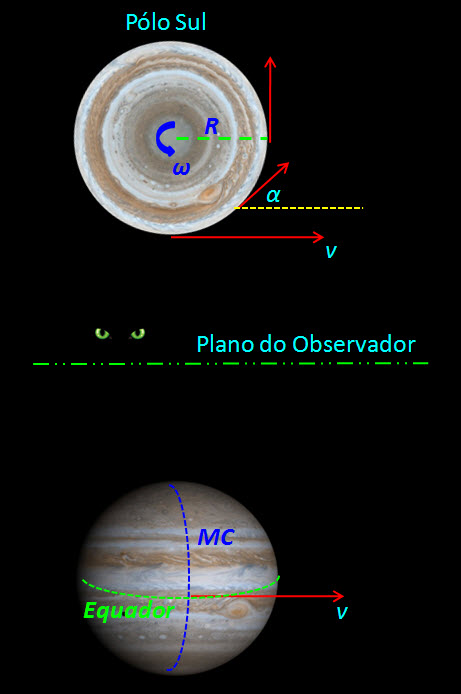
Figura 1. Planeta vista superior do pólo (acima) e vista de frente (abaixo). R é o raio aparente do planeta em segundos de arco, ω é a velocidade angular, v é a velocidade linear, CM é o Meridiano Central.
Seja R o raio aparente do planeta, em segundo de arco, que rotaciona sobre o seu eixo em uma velocidade angular ω, proveniente do período de rotação. A velocidade angula se traduz na velocidade linear v cujo módulo é:
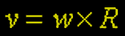
Como o disco do planeta projeta-se sobre o plano do observador, somente o componente paralelo à este último é considerado. Este componente tem seu pico no centro do disco planetário e reduz em direção a borda do planeta onde a distorção geométrica distorce a visibilidade dos detalhes da superfície. A componente da velocidade ao longo do plano de observação pode ser calculado por:
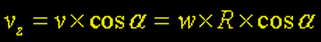
que atinge seu valor máximo para α igual a zero (α=0), resultando em:
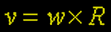
Para ângulos pequenos, podemos utilizar:
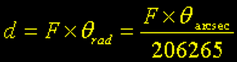
onde:
- θ é o diâmetro angular aparente do objeto (radianos ou segundos de arco);
- F é a distância focal do telescópio e;
- d é o tamanho linear da imagem projetada sobre o sensor.
As mesmas unidades devem ser utilizadas para os valores de F e d, normalmente, milímetros (mm). Podemos assumir o valor de d
como o deslocamento máximo permissível ao disco do planeta antes que sua rotação deteriore nossa imagem, isto é, se o deslocamento não for maior que um único pixel, este não será detectável na imagem fotográfica. Re-escrevendo a equação acima, temos:
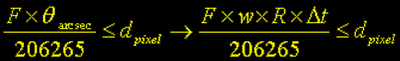
resultando em:
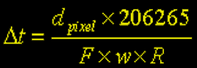
Exemplo:
Consideremos o seguinte caso: desejamos fotografar Marte, Júpiter e Saturno em oposição, isto é, no tempo de seu maior e melhor tamanho angular. No caso de Saturno, consideramos o tamanho angular do disco do planeta, não incluindo os anéis. Vamos considerar que estamos utilizando uma câmera cujo o sensor ccd é do tipo Sony ICX, encontrado em câmeras como Celestron, Atik, e outras. Este tipo de chip possui pixels com 5.6 µ (5.6 micra ou 0.0056 mm).
Vamos considerar ainda que utilizaremos um telescópio Schimit-Cassegrain, 200 mm de abertura, F/10, com uma barlow 3X, resultando em uma distância focal efetiva (DFE) de 6000 mm.
A velocidade angular do planeta pode ser obtida com a seguinte equação:
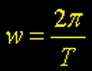
onde T é o período de rotação do planeta em segundos.
Aplicando a equação acima, podemos montar a seguinte tabela:

Para os gigantes gasosos, consideramos o sistema equatorial que é o mais veloz. Na tabela acima podemos observar que aproximadamente 4 minutos para Marte, 1 minuto para Júpiter e 2 minutos para Saturno são teoricamente os limites máximos de tempo de filmagem; entretanto, na prática há sempre alguma diferença.
Os valores de 3 a 4 minutos para Marte são razoáveis. Para Júpiter, em média, um filme de 15 FPS de um minuto de duração contém poucos dados. Assim, podemos aumentar esse limite para 100 a 120 segundos com uma leve deterioração da imagem (praticamente indetectável) mas com muito mais informação que beneficia o resultado final. Já para Saturno, um filme de 2 minutos pode ser suficiente, uma vez que os detalhes de sua superfície são menos complexos que os de Júpiter.
Um ponto crítico é a fotografia colorida de Júpiter utilizando o sistema LRGBC. São necessários pelos menos três filmes (RGB) para a fotografia colorida. Um ccd com pixel de 5.6 µ de tamanho em um sistema com 6000 mm de distância focal implica em uma resolução de 0.19 arco segundo, a qual esta bem abaixo do poder de resolução da maioria dos equipamentos utilizados por amadores e das condições de visão em uma típica noite. Isto permite que aumentemos esse tempo entre 80 a 100% do valor teórico e ainda assim obtermos uma imagem aceitável.
Os outros planetas (Mercúrio, Venus, Urano e Netuno) não apresentam muitos detalhes de superfície e são pequenos o bastante para não implicar em qualquer alteração. De qualquer modo, deve-se ficar atento para outros fatores que possam impactar na qualidade da fotografia como, por exemplo, erro periódico da montagem, imprecisão de alinhamento polar e outros. O problema pode ser agravado na fotografia RGB com o tempo gasto na troca de filtros e refocalização.
Este modelo assume algumas simplificações e assim pode ser aprimorado. Por exemplo, assumiu-se o centro do planeta como o ponto de movimento mais veloz do sistema. Isto não é totalmente verdadeiro, uma vez que o ponto mais veloz cai numa região onde ocorre a interseção do equador com o meridiano central do planeta. Esta área será a mesma do centro geométrico do disco planetário somente se o eixo de rotação se situar exatamente no plano de observação sendo assim ortogonal a linha de visão. Isto não se aplica se a inclinação do eixo tiver um componente ao longo da linha de visão como é o caso de Saturno e Marte.
O método aqui descrito é baseado no pior caso, isto é, a interseção do meridiano central com o equador do planeta alvo da fotografia. Assim, os dobros dos tempos calculados ainda produziram fotografias aceitáveis na prática.
Outro detalhe é o teorema de Nyquist/Shannon que estabelece que uma amostra utilizando um sinal analógico limitado pela banda pode ser reconstruído somente se a freqüência de amostragem é ao menos duas vezes tão grande quanto a largura de banda do sinal. Em uma imagem 2-D isto significa que o tamanho do pixel não deve ser maior que a metade do tamanho do menor detalhe que se deseja capturar. Colocando de outro modo: o tamanho do menor detalhe distinguível é de dois pixels.
Entretanto este critério somente se aplica para condições ideais onde o ruído é ausente ou ao menos negligenciável. Por outro lado, tomadas únicas com sensores não resfriados (como no caso de se utilizar webcams) podem ser severamente degradadas pelo ruído e ter uma relação sinal/ruído extremamente baixa. O problema pode ser parcialmente contornado por empilhar muitos fotogramas, mas geralmente serão necessários mais do que dois pixels. Assim, oversampling por aumento da distância focal equivalente será de grande ajuda.
Este método se aplica apenas a sensores monocromáticos onde cada pixel amostra o sinal de entrada e realiza sua contribuição para a imagem final. Os sensores que utilizam a matriz de Bayer (coloridos), a qual consiste de microlentes de uma cor primária, faz com que cada pixel veja apenas uma cor de três existentes. As outras duas cores descartadas são processadas por interpolação dos valores de pixels próximos. Isto reduz o custo do chip, mas as custas de redução da resolução.


